Cyrano Sciences' Sensor Technology
The Heart of the Cyranose® 320
by: Erik Severin
Cyrano Sciences' propriety sensor technology, used in the Cyranose® 320, originated in the labs of Professor Nathan Lewis at the California Institute of Technology. The technology consists of individual thin-film carbon-black polymer composite chemiresistors configured into an array. The collective output of the array is used to identify an unknown analyte using standard data analysis techniques. The sensor array, along with data analysis algorithms, form the main components of Cyrano's electronic nose.
Each individual detector of the sensor array is a composite material consisting of conductive carbon black homogeneously blended throughout a non-conducting polymer. The detector materials are deposited as thin films on an alumina substrate each across two electrical leads creating conducting chemiresistors. The output from the device is an array of resistance values as measured between each of the two electrical leads for each of the detectors in the array.
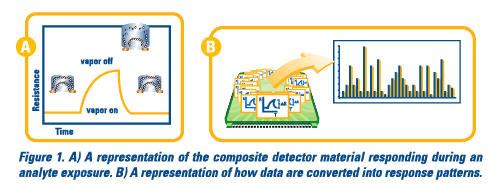
When a composite is exposed to a vapor-phase analyte, the polymer matrix acts like a sponge and "swells up" while absorbing the analyte. The increase in volume is concomitant with an increase in resistance because the conductive carbon-black pathways through the material are broken. When the analyte is removed, the polymer "sponge" off-gasses and "dries out". This causes the film to shrink and the conductive pathways are reestablished. The baseline resistance (Rbaseline) of the device is measured while a representative background vapor flows over the array. The response from the chemiresistor during an analyte exposure is measured as a bulk relative resistance change ( Rmax/Rbaseline). Since an analyte will absorb into the different polymer matrices to different degrees, a pattern of response is observed across the array.
Rmax/Rbaseline). Since an analyte will absorb into the different polymer matrices to different degrees, a pattern of response is observed across the array.
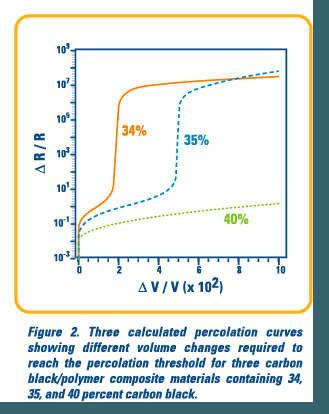
The relationship between volume increase and the resistance change in these composite films can be described by percolation theory.1 Percolating networks are ubiquitous in nature and are based on the idea that certain phenomena propagate through a system by interactions between neighboring active sites. Examples include forest fires spreading from tree to tree, disease spreading through a population by human contact, sol-gel transitions in biopolymer gelation, and, as in this case, resistor networks that are either continuous, and connected, or discontinuous.2
In percolating resistor networks, there is a critical point where the last conductive pathway is broken and the system becomes discontinuous. This point is called the percolation threshold and is highly dependent on system variables. In the case of carbon black polymer composites, the percolation threshold is reached when an individual detector's resistance sharply increases with a small increase in volume of the composite film. The form of a percolation curve is very similar to a pH titration curve. The change in volume required to reach the percolation threshold for a given detector is dependent on the amount of carbon black in the polymer matrix, the structure of that carbon black, the degree of contact between carbon black clusters, and how homogeneously dispersed are the carbon black clusters through the matrix.
The polymer matrix "swells up" because analyte vapor absorbs into the film to an extent determined by the partition coefficient of the analyte. The partition coefficient defines the equilibrium distribution of an analyte between the vapor phase and the condensed phase at a specified temperature. This is expressed as,
K = Cs/Cv (1)
where Cv is the concentration of the analyte in the vapor phase, and Cs is the concentration of the analyte in the condensed phase, which is also proportional to the detector's response. Therefore, the larger an analyte's partition coefficient, the more it will absorb into a polymer film, and the larger will be the detector's response.
Each individual detector element requires a minimum absorbed amount of analyte (Cs,min) to cause a response noticeable above the baseline noise. However, the minimum vapor concentration (Cv,min) needed to produce Cs,min is different for each analyte since the partition coefficient is different for each analyte. Moreover, it can be shown with standard thermodynamic arguments, that the magnitude of response of an individual detector can be predicted to first order by the fractional vapor pressure exposed to the detector irrespective of the analyte identity.3, 4 Therefore, the general detection limit of a sorption device is best expressed as a minimum fraction of equilibrium vapor pressure rather than a concentration value.
This behavior explains why sorption devices are rather insensitive, in terms of concentration, to high vapor pressure analytes like methane (which is a gas at ambient temperatures) and diethyl ether, but show good sensitivity, in terms of concentration, to low vapor pressure compounds exposed at low concentrations such as volatile fatty acids. For example, if the limit of detection were 0.1% of an analyte's vapor pressure, this would indicate a detection limit of 74 ppm for ethanol, but only 0.5 ppm for nonanal (a common taint in packaging materials) at 24°C. All analytes will have roughly the same limit of detection when expressed as a fractional vapor pressure.
The differences between detector responses when exposed to a given analyte - which are required to uniquely identify that analyte by providing a unique response pattern - are due to differences in chemical interactions between the analyte and the detector films. Therefore, the limit of discrimination between two analytes exposed at the same fractional vapor pressure is determined by their relative collective chemical differences across the array. This indicates the need for as much chemical diversity as possible in the polymers comprising the array detectors for a general-purpose electronic nose. Moreover, for well-defined applications, the polymers used in the detector array can be chosen to maximize chemical differences between target analytes to increase the discrimination power of a smaller array.
This underscores the power of Cyrano Sciences' polymer composite sensor technology because it is not reliant on any particular polymer type or limited to a particular set of polymers. Additionally, the simplicity of signal transduction (merely reading resistance values) and the low materials cost of the detectors (composites made of carbon black and generic polymers) makes this an ideal technology for a low-cost, hand-held, electronic nose.
- Lonergan, M. C.; Severin, E. J.; Doleman, B. J.; Beaber, S. A.; Grubbs, R. H.; Lewis, N. S. Chem. Mater. 1996, 8, 2298
- Stauffer, D.; Aharony, A.; Introduction to Percolation Theory; Taylor & Francis: Bristol, PA, 1994
- Atkins, P. W.; Physical Chemistry; W.H. Freeman and Co.: New York, NY, 1994
- Doleman, B. J.; Severin, E. J.; Lewis, N. S. Proc. Natl .Acad. Sci .,USA 1998, 95, 5442



